حل معادلات درجه دوم
روش های حل معادله درجه دو بهطور ویژه در فصل 4 ریاضی دهم تجربی مورد بررسی قرار میگیرد. معادله درجه 2 را میتوان با روشهای مختلفی حل کرد. مانند روش مربع کامل، ریشهگیری، تجزیه، روش دلتا (فرمول کلی) و….
برای حل این دسته از معادلات، اولویت، انتخاب روش تجزیه است. اگر این روش امکانپذیر نبود، بهترین انتخاب، فرمول کلی یا روش دلتا است. همچنین یکی از موارد پرکاربرد در ریاضیات، مبحث روابط بین ریشه های معادله درجه دو است. در این آموزش به این موضوع نیز پرداختهایم. جهت تسلط در حل این نوع معادلات و کاربردهای آن حتما مقاله را تا انتها مطالعه کنید.
همانطور که میدانید سهمی و معادله درجه دوم با هم ارتباط مستقیمی دارند. لذا به شما پیشنهاد میدهم حتما مقاله بسیار جامع و مفید آموزش سهمی دهم را نیز مطالعه بفرمایید.

فهرست مطالب
واژههای تخصصی معادله درجه دو
- معادلات درجه دوم: Quadratic Equations
- روش مربع کامل : Complete The Square - Method
- روش ریشه گیری : Square Roots - Method
- روش دلتا : Quadratic Formula - Method
- روش تجزیه : Factoring - Method
- تجزیه : Decomposition
- ریشه: Root
فهرست مطالب
واژههای تخصصی معادله درجه دو
- معادلات درجه دوم: Quadratic Equations
- روش مربع کامل : Complete The Square - Method
- روش ریشه گیری : Square Roots - Method
- روش دلتا : Quadratic Formula - Method
- روش تجزیه : Factoring - Method
- تجزیه : Decomposition
- ریشه: Root
روش های حل معادله درجه دو
فرم کلی معادله درجه 2 بهصورت \(\LARGE ax^2+bx+c=o\) است. در این معادله \(\LARGE a\) و \(\LARGE b\) و \(\LARGE c\) اعداد حقیقی هستند و \(\LARGE a≠0\) .
برای حل این دسته از معادلات روشهای مختلفی وجود دارد. در ادامه تعدادی از این روشها را شرح میدهیم.
همین حالا در آزمون آنلاین فصل 4 ریاضی دهم تجربی شرکت کنید.
روش تجزیه
معادلهی \(\LARGE ax^2+bx+c=o\) را در نظر میگیریم. دراین روش، عبارت \(\LARGE ax^2+bx+c\) را از طریق فاکتورگیری یا به کمک اتحادها تجزیه میکنیم. سپس عبارت تجزیهشده را در معادلهی اولیه قرار داده و آن را حل میکنیم. برای درک بهتر به مثالهای زیر توجه کنید:
مثال 1. معادلهی \(\LARGE x^2-2x-3=o\) را از روش تجزیه حل کنید.
ابتدا با استفاده از اتحاد یک جمله مشترک معادله داده شده را بهصورت زیر تجزیه میکنیم:
\[\LARGE{(x-3)(x+1)=0}\]
میدانیم هرگاه حاصلضرب دو عبارت صفر باشد هرکدام از آنها میتوانند صفر باشند. یعنی:\[\LARGE\begin{cases}x-3=0 \\x+1=0\ \end{cases}⇒\begin{cases}x=3 \\x=-1\ \end{cases}\]
مشاهده میکنیم معادله دو ریشهی حقیقیِ متمایز دارد.
مثال 2. معادلهی \(\LARGE 3t^2-t=o\) را با روش بالا حل کنید.
ابتدا با استفاده از فاکتورگیری معادله داده شده را تجزیه میکنیم:
\[\LARGE{t(3t-1)=0}\] حاصلضرب دو عبارت صفر است. هرکدام آنها میتواانند صفر باشند:\[\LARGE\begin{cases}t=0 \\3t-1=0⇒ t=\frac{1}{3}\ \end{cases}\]
این معادله هم دو ریشهی حقیقیِ متمایز دارد.

روش ریشه گیری
معادلهی \(\LARGE x^2=a\) را در نظر میگیریم. توجه داریم ضریب \(\large x^2\) باید یک و \(\LARGE a\) مثبت باشد. برای حل آن از طریق ریشهگیری کافی است از طرفین جذر بگیریم. در نتیجه:\[\LARGE{\sqrt{x^2}=\left| x\right|=\sqrt{a}\ ⇒\ x=±\sqrt{a} }\]
مثال 3. معادلهی \(\LARGE 5x^2=20\) را با روش ریشه گیری حل کنید.
با کمی دقت به این نکته پی میبریم در این معادله ضریب \(\LARGE x^2\) یک نیست. کافی است طرفین را بر 5 تقسیم کنیم:
\[\LARGE{5x^2=20\ ⇒\ x^2=4\ ⇒\ x=±2 }\]
مثال 4. معادلهی \(\LARGE t^2+7=o\) را با استفاده از ریشه گیری حل کنید.
\[\LARGE{t^2+7=0\ ⇒\ t^2=-7}\]
این معادله جواب حقیقی ندارد. زیرا یک عبارت درجه دوم نمیتواند مقدار منفی بپذیرد.
نکته مهم
\(\LARGE \sqrt{x^2}=\left|x \right|\)
روش مربع کامل
میدانیم اتحاد مربع مجموع دو جمله بهصورت زیر است:
\[\LARGE{(a+b)^2=a^2+2ab+b^2 }\]
برای حل معادله با روش مربع کامل، تلاش میکنیم آن را با انجام ترفندهایی، به اتحاد مربع مجموع دو جمله تبدیل کنیم. در پایان میتوانیم جواب معادلهای که بهدست آمده است را با روش ریشهگیری محاسبه کنیم.
به این نکته بسیار مهم توجه کنید! برای استفاده از روش مربع کامل باید ضریب \(\LARGE x^2\) یک باشد.
برای درک بهتر این روش به مثال زیر دقت کنید.
مثال 5. قصد داریم معادلهی \(\LARGE x^2-6x+4=o\) را با استفاده از روش مربع کامل حل کنیم.
گام اول. ابتدا عدد 4 را سمت راست معادله منتقل میکنیم.
\[\LARGE{x^2-6x=-4}\]
گام دوم. سپس ضریب \(\LARGE x\) را بر 2 تقسیم و عدد بهدست آمده را به توان دو میرسانیم.
\[\Large{\frac{-6}{2}=-3}\] \[\Large{(-3)^2=9}\]
گام سوم. عدد نهایی که در این مثال 9 است را به طرفین معادلهی گام اول اضافه میکنیم.
\[\Large{x^2-6x+9=-4+9}\]
\[\Large{x^2-6x+9=5}\]
گام چهارم. حال با کمی دقت متوجه میشویم سمت چپ معادلهی بالا (گام سوم) قابل تجزیه به اتحاد مربع مجموع دو جمله است.
\[\Large{(x-3)^2=5}\]
گام پنجم. کافی است از طرفین معادلهی نهایی بالا جذر بگیریم. در واقع روش ریشهگیری را بهکار میبریم.
\[\Large\sqrt{(x-3)^2}=\sqrt{5}\]
\[\Large{\left| x-3\right|=\sqrt{5}}\]\[\Large{x-3=±\sqrt{5}}\]
در نتیجه:\[\Large\begin{cases}x-3=\sqrt{5} \\x-3=-\sqrt{5}\ \end{cases}\]
\[\Large\begin{cases}x=3+\sqrt{5} \\x=3-\sqrt{5}\ \end{cases}\]
بهعبارتی معادله دارای دو جواب حقیقیِ متمایز است.
سخته؟؟ درست شنیدم؟! میخواید یه مثال دیگه هم حل کنیم با هم؟ خلاصه تا یاد نگرفتین اینو، نباید رد شید برید هااااا! تازه در پایان مقاله هم براتون مشق شب گذاشتم. حلشون کنین بیاین جوابارو بگین تو کامنتا.
مثال 6. معادلهی \(\LARGE 3x^2-12x-1=o\) را از روش مربع کامل حل کنید.
ابتدا باید طرفین را بر ضریب \(\LARGE x^2\) یعنی 3 تقسیم کنیم تا ضریب \(\LARGE x^2\) طبق نکتهی بالا یک شود.
\[\LARGE{x^2-4x-\frac{1}{3}=0}\]
در واقع با معادلهی اولیه خداحافظی میکنیم و در ادامه با \(\LARGE x^2-4x-\frac{1}{3}=0\) سر و کار داریم.
گام اول. ابتدا عدد \(\LARGE \frac{1}{3}\) را سمت راست معادله منتقل میکنیم.
\[\LARGE{x^2-4x=\frac{1}{3}}\]
گام دوم. سپس ضریب \(\LARGE x\) را بر 2 تقسیم و عدد بهدست آمده را به توان دو میرسانیم.
\[\LARGE{\frac{-4}{2}=-2}\] \[\LARGE{(-2)^2=4}\]
گام سوم. عدد نهایی که در این مثال 4 است را به طرفین معادلهی گام اول اضافه میکنیم.
\[\LARGE{x^2-4x+4=\frac{1}{3}+4}\]
\[\LARGE{x^2-4x+4=\frac{13}{3}}\]
گام چهارم. حال با کمی دقت متوجه میشویم سمت چپ معادلهی بالا (گام سوم) قابل تجزیه به اتحاد مربع مجموع دو جمله است.
\[\LARGE{(x-2)^2=\frac{13}{3}}\]
گام پنجم. کافی است از طرفین معادلهی نهایی بالا جذر بگیریم. در واقع روش ریشهگیری را بهکار میبریم.
\[\LARGE\sqrt{(x-2)^2}=\sqrt{\frac{13}{3}}\]
\[\LARGE{\left| x-2\right|=\sqrt{\frac{13}{3}}}\]\[\LARGE{x-2=±\sqrt{\frac{13}{3}}}\]
در نتیجه:\[\LARGE\begin{cases}x-2=\sqrt{\frac{13}{3}} \\x-2=-\sqrt{\frac{13}{3}}\ \end{cases}\]
\[\LARGE\begin{cases}x=2+\sqrt{\frac{13}{3}} \\x=2-\sqrt{\frac{13}{3}}\ \end{cases}\]
بهعبارتی معادله دارای دو جواب حقیقیِ متمایز است.
روش دلتا (فرمول کلی)
جهت استفاده از روش دلتا گامهای زیر را دنبال میکنیم:
گام اول. برای معادلهی \(\LARGE ax^2+bx+c=o\) فرمول زیر که به فرمول دلتا معروف است را تشکیل میدهیم:
\[\LARGE{Δ=b^2-4ac}\]
گام دوم. برای \(\LARGE Δ\) که یک مقدار عددی است، سه حالت رخ میدهد:
- \(\LARGEΔ>0\)، در این حالت معادلهی درجه دوم دارای دو ریشهی حقیقی و متمایز است. این دو ریشه از فرمولهای زیر بهدست میآیند:
\[\LARGE\begin{cases}x_1=\frac{-b+\sqrt{Δ}}{2a}\ \\x_2=\frac{-b-\sqrt{Δ}}{2a}\ \end{cases}\]
- \(\LARGEΔ=0\)، در اینصورت معادله دارای یک ریشهی مضاعف است و فرمول محاسبهی آن بهصورت:
\[\LARGE{x=\frac{-b}{2a}}\]
است.
- \(\LARGEΔ<0\)، در این حالت معادله ریشهی حقیقی ندارد.
به این نکته بسیار مهم توجه کنید! برای استفاده از روش دلتا باید سمت راست معادله صفر باشد.
مثالهای روش دلتا
مثال 7. معادلات زیر را از روش دلتا حل کنید.
الف) \(\LARGE{t^2-3t+3=0}\)
حل:
\[\LARGE{Δ=b^2-4ac}\]
\[\LARGE{Δ=(-3)^2-4(1)(3)=-3}\]
\[\LARGE{Δ<0}\]
در نتیجه معادله دارای جواب حقیقی نیست.
ب) \(\LARGE{x^2-6x=7}\)
حل:
\[\LARGE{x^2-6x-7=0}\]
\[\LARGE{Δ=b^2-4ac}\]
\[\LARGE{Δ=(-6)^2-4(1)(-7)=64}\]
\[\LARGE{Δ>0}\]
لذا معادله دارای دو جواب حقیقیِ متمایز است :
\[\LARGE\begin{cases}x_1=\frac{-b+\sqrt{Δ}}{2a}\ \\x_2=\frac{-b-\sqrt{Δ}}{2a}\ \end{cases}\]
در نتیجه:
\[\LARGE\begin{cases}x_1=\frac{6+\sqrt{64}}{2}=7\ \\x_2=\frac{6-\sqrt{64}}{2}=-1\ \end{cases}\]
ج) \(\LARGE{s^2+4s+4=0}\)
حل:
\[\LARGE{Δ=b^2-4ac}\]
\[\LARGE{Δ=(4)^2-4(1)(4)=0}\]
\[\LARGE{Δ=0}\]
بنابراین معادله دارای ریشه مضاعف زیر است:
\[\LARGE{s=\frac{-b}{2a}=\frac{-4}{2}=-2}\]
روابط بین ریشه های معادله درجه دو
فرض کنید معادله درجه 2 دارای دو ریشهی حقیقی و متمایز \(\LARGE x_1\) و \(\LARGE x_2\) است. منظور از رابطه بین ریشه های معادله درجه دو، محاسبه حاصل جمع و حاصل ضرب ریشه ها از فرمول زیر است:
حاصل جمع ریشهها: \(\LARGE{S=\frac{-b}{a}}\)
حاصل ضرب ریشهها: \(\LARGE{P=\frac{c}{a}}\)
مثال 8. حاصل جمع و حاصل ضرب ریشههای معادله درجه دو \(\LARGE 4x^2-13x+3=0\) را در صورت وجود تعیین کنید.
ابتدا با محاسبهی \(\LARGE Δ\) درمییابیم مقدار آن 121 است. در واقع \(\LARGE Δ>0\) است. لذا معادله دارای دو جواب حقیقیِ متمایز است و:
حاصل جمع ریشهها: \(\LARGE{S=\frac{-b}{a}=\frac{13}{4}}\)
حاصل ضرب ریشهها: \(\LARGE{P=\frac{c}{a}=\frac{3}{4}}\)
یافتن معادله درجه دو بهکمک حاصل جمع و حاصل ضرب ریشهها
حال بالعکس، فرض کنید حاصلجمع و حاصلضرب ریشههای معادلهی درجه دوم یعنی \(\LARGE S\) و \(\LARGE P\) را داریم. قصد ما این است که با استفاده از آنها معادلهی مورد نظر را بیابیم. کافیست از فرمول زیر استفاده کنیم:
\[\LARGE{x^2-Sx+P=0}\]
مثال 9. حاصلجمع و حاصلضرب ریشههای یک معادلهی درجه دوم بهترتیب 5 و 3- است. معادلهی موردنظر را بیابید.
\[\LARGE{x^2-Sx+P=0}\]
\[\LARGE{x^2-5x-3=0}\]
مشق شب برای شما
مشق اول .
معادلات درجه دوم زیر را با روشهای خواستهشده حل کنید.
- \[\LARGE{x-x^2=3}\] (روش دلتا)
- \[\LARGE{9-6z+z^2=0}\] (روش تجزیه)
- \[\LARGE{2x^2=250}\] (روش ریشه گیری)
- \[\LARGE{t^2-\sqrt{t}-4=0}\] (روش مربع کامل)
مشق دوم . اگر \(\LARGE x_1\) و \(\LARGE x_2\) ریشههای معادلهی \(\LARGE 3x^2-x-3=0\) باشند، مجموع مربعات ریشهها را بهدست آورید.
مشق سوم . معادلهای را بیابید که ریشههای آن \(\LARGE a+\frac{1}{a}\) و \(\LARGE a-\frac{1}{a}\) است.
پاسخهای خود را در بخش نظرات ارسال فرمایید.
اگر در حل این سؤالات یا بطور کلی در یادگیری مبحث معادله درجه دوم با چالش مواجهید برای بهره بردن از کلاسهای خصوصی آنلاین در سراسر کشور یا خارج از ایران و کلاسهای حضوری ویژهی مشهد با ما تماس بگیرید.
نظرات در بارهی "روش های حل معادلات درجه دوم"
واژههای تخصصی معادله درجه دو
- معادلات درجه دوم: Quadratic Equations
- روش مربع کامل : Complete The Square - Method
- روش ریشه گیری : Square Roots - Method
- روش دلتا : Quadratic Formula - Method
- روش تجزیه : Factoring - Method
- تجزیه : Decomposition
- ریشه: Root
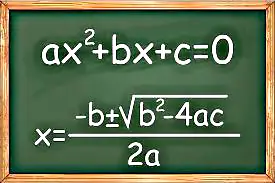
این مطلب عاااالی بود.واقعا یاد گرفتم مبحثشو. ممنون از شما
سلام دوست عزیز!
خوشحالم که مطلب مفید واقع شده.
سپاس بابت همراهی شما